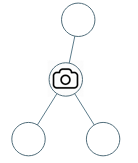
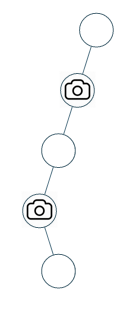
968. Binary Tree Cameras

Given a binary tree, we install cameras on the nodes of the tree.

Each camera at a node can monitor its parent, itself, and its immediate children.

Calculate the minimum number of cameras needed to monitor all nodes of the tree.

Example 1:

Input: [0,0,null,0,0]
Output: 1
Explanation: One camera is enough to monitor all nodes if placed as shown.

Example 2:

Input: [0,0,null,0,null,0,null,null,0]
Output: 2
Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.

Note:

1. The number of nodes in the given tree will be in the range [1, 1000].

2. Every node has value 0.

// DFS Recursion
// 0: has a leaf child uncoved
// 1: a leaf parentwith camera
// 2: covered without camera
int helper(TreeNode* node, int& res) {
    if (!node) return 2;
    int left = helper(node->left, res), right = helper(node->right, res);
    if (left == 0 || right == 0) {
        ++res;
        return 1;
    }
    return (left == 1 || right == 1) ? 2 : 0;
}
int minCameraCover(TreeNode* root) { // time: O(n); space: O(n)
    int res = 0;
    if (helper(root, res) < 1) ++res;
    return res;
}