235. Lowest Common Ancestor of a Binary Search Tree

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]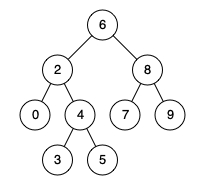

Example 1:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Note:

• All of the nodes' values will be unique.

• p and q are different and both values will exist in the BST.

// Recursion
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { // time: O(n); space: O(n)
    if (root->val > p->val && root->val > q->val) 
        return lowestCommonAncestor(root->left, p, q);
    else if (root->val < p->val && root->val < q->val) 
        return lowestCommonAncestor(root->right, p, q);
    return root;
}

// Iteration
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { // time: O(n); space: O(1)
    TreeNode* cur = root;
    while (cur) {
        if (cur->val > p->val && cur->val > q->val) 
            cur = cur->left;
        else if (cur->val < p->val && cur->val < q->val)
            cur = cur->right;
        else
            break;
    }
    return cur;
}