1192. Critical Connections in a Network

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

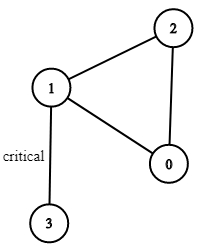
Constraints:

• 1 <= n <= 10^5

• n-1 <= connections.length <= 10^5

• connections[i][0] != connections[i][1]

• There are no repeated connections.

// Tarjan's Algorithm
void dfs(int u, int pre, int& time, vector<int>& disc, vector<int>& low, vector<vector<int> >& graph, vector<vector<int> >& res) {
    disc[u] = low[u] = ++time; // discover u
    for (int v : graph[u]) {
        // if v is parent vertex, skip
        if (v == pre) continue;
        // v is not visited yet
        if (disc[v] == -1) {
            dfs(v, u, time, disc, low, graph, res);
            low[u] = min(low[u], low[v]);
            // u -> v is critical, there is no path for v to reach back to u or previous vertices of u
            if (low[v] > disc[u]) {
                res.push_back({u, v});
            }
        }
        // v is discovered but is not parent of u, it means v is included in the previously found subtree
        // update low[u], cannot use low[v] because u is not subtree of v
        else {
            low[u] = min(low[u], disc[v]);
        }
    }
}
vector<vector<int> > criticalConnections(int n, vector<vector<int>>& connections) { // time: O(V + E); space: O(V + E)
    vector<int> disc(n, -1), low(n, 0);
    vector<vector<int> > graph(n), res;
    // Build adjacency list
    for (const auto& edge : connections) {
        graph[edge[0]].emplace_back(edge[1]);
        graph[edge[1]].emplace_back(edge[0]);
    }
    int time = 0; // discovery time
    dfs(0, 0, time, disc, low, graph, res);
    return res;
}