52. N-Queens II

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

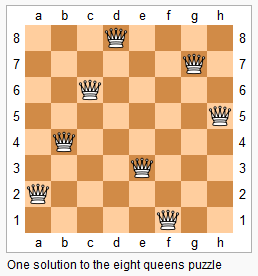
Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example:

Input: 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown below.
[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

In first method, pos[i] represents the column location of the i row.

bool isValid(vector<int>& pos, int row, int col) {
    for (int i = 0; i < row; ++i) {
        if (col == pos[i] || abs(row - i) == abs(col - pos[i])) return false;
    }
    return true;
}
void helper(vector<int>& pos, int row, int& res) {
    int n = pos.size();
    if (row == n) ++res;
    else {
        for (int col = 0; col < n; ++col) {
            if (isValid(pos, row, col)) {
                pos[row] = col;
                helper(pos, row + 1, res);
                pos[row] = -1;
            }
        }
    }
}
int totalNQueens(int n) { // time: O(n^2); space: O(n^2)
    int res = 0;
    vector<int> pos(n, -1);
    helper(pos, 0, res);
    return res;
}

In the second method, a flag array is used to record the location on the column, 45 degree diagonal, 135 degree diagonal. It can be separated into three flag arrays. 1. flag_col with the size of n 2. flag_45 with the size of 2 * n - 1 3. flag_135 with the size of 2 * n - 1 We need to check them when reaching location (row, col) by flag_col[col], flag_45[row + col], and flag_135[n - 1 + col - row]. Finally, three flag arrays can be combined into one, which has the size of 5 * n - 2. For column checking => flag[col]

for 45-degree diagonal checking => flag[n + row + col]

for 135-degree diagonal checking => flag[n + 2 * n - 1 + n - 1 + col - row]

The following explanation comment is copied from https://leetcode.com/problems/n-queens/discuss/19808/Accepted-4ms-c++-solution-use-backtracking-and-bitmask-easy-understand.

/**    | | |                / / /             \ \ \
  *    O O O               O O O               O O O
  *    | | |              / / / /             \ \ \ \
  *    O O O               O O O               O O O
  *    | | |              / / / /             \ \ \ \ 
  *    O O O               O O O               O O O
  *    | | |              / / /                 \ \ \
  *   3 columns        5 45° diagonals     5 135° diagonals    (when n is 3)
  */

void helper(int& res, vector<int>& flag, int row, int n) {
    if (row == n) ++res;
    else {
        for (int col = 0; col < n; ++col) {
            if (flag[col] && flag[n + row + col] && flag[n + 2 * n - 1 + n - 1 + col - row]) {
                flag[col] = flag[n + row + col] = flag[4 * n - 2 + col - row] = 0;
                helper(res, flag, row + 1, n);
                flag[col] = flag[n + row + col] = flag[4 * n - 2 + col - row] = 1;
            }
        }
    }
}
int totalNQueens(int n) { // time: O(n^2); space: O(n^2)
    int res = 0;
    vector<int> flag(5 * n - 2, 1);
    helper(res, flag, 0, n);
    return res;
}